Sensitivity and the Single Source

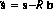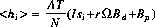
For a coded aperture camera illuminated by a single source and background, the expected number of counts in each detector element is given by:

where:

$I$ is the source intensity.
$r$ is the rato of pinhole area to detector area.
$N$ is the number of elements in the position senstive detector.
$A$ is the detector area.
$T$ is the integration time.
$B sub d$ is the diffuse background rate.
$B sub p$ is the intrinsic detector background rate.
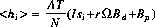
$OMEGA$ is the solid angle of the detector, as seen from the aperture.

In the case of a dominant, known background, the matched filter method can be used to estimate $I$ from the data. The total background per detector element is:

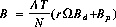
To implement the matched filter, the background must be subtracted from $bold h$, yielding $bold h prime$:

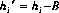
The matched filter vector is then given by:

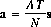
and the estimated intensity is:

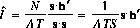
where:

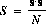
$S$ is the "power" in the shadow pattern (in a mathematical rather than a physical sense).

Assuming that the background dominates the noise, the signal to noise ratio may be approximated by:

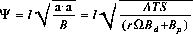
If the projected aperture lies entirely within the boundary of the detector and the observed shadow pattern is perfectly sharp, $S ~=~ r$. If in addition the particle background is a negligible contributer to the noise, $r$ drops out of the signal to noise equation:

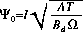
$PSI sub 0$ represents an upper limit on the sensitivity of the coded aperture system.

If the background is uncertain, the expected detector response may be written as:

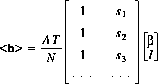
where:

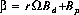
I'll call the first column of the detector response matrix the "background vector", or $bold b$; $b sub i = 1$ for all $i$. The least squares estimates of $I$ and $beta$ may be obtained by solving the equation:

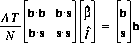
At this point, it is convenient to introduce two more definitions:

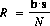
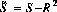
$R$ is the average value in the shadow pattern $bold s$; thus $R sup 2$ is the portion of the power in the shadow pattern due to its nonzero average (the "DC" power), and $S tilde$ is the rest of the power in the shadow pattern (the "AC" power). Rewriting the least squares equation in terms of $R$ and $S$ (also noting that $bold b cdot bold b = N$):

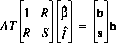
The solution is:

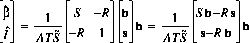
The estimated source intensity is:

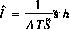
where: